Logic-trees#
The logic-tree is an integral component of a PSHA input model for the OpenQuake engine. An OpenQuake engine input model always contains a logic tree structure describing the epistemic uncertainties associated with the construction of the seismic source model and a logic-tree used to formally specify the epistemic uncertainties related to the GSIM models used in different tectonic regions for the calculation of hazard.
The definition of logic trees in the OpenQuake engine is based on the combination of a number of predefined modules, each one modelling a specific epistemic uncertainty (see the figure below for a schematic describing this particular feature). This approach brings a number of advantages. The first and most obvious is that the user is not forced to use a predefined logic tree structure and - instead - can create a tailored logic tree which integrally reflects the specific uncertainties they want to model. The second is that the logic tree structure becomes an integral part of a PSHA input model definition. The hazard calculations based on this approach are testable, fully reproducible and do not require pre- or post-processing steps since these are features included in the engine.
This Chapter is dedicated to the description of the basic theory behind logic-trees and to the delineation of how logic-trees are implemented into the OpenQuake engine.
Introduction#
The use of logic-trees to account for epistemic uncertainties in probabilistic seismic hazard analysis was originally proposed by Kulkarni et al. (1984). Nowadays logic-trees are an essential component of a PSHA input model and represent the formal methodology though which is possible to synthesize the outcomes of the elicitation process on epistemic uncertainties requested in site-specific seismic hazard analyses (Budnitz et al., 1997) as well as for the creation of state-of-the-art national and regional PSHA input models.
The interpretation of the branches in a logic tree structure, of their corresponding weights and of the related results is still the subject of an intense scientific debate going on in the literature since 2005 (Abrahamson and Bommer, 2005; McGuire et al., 2005; Musson, 2012; Scherbaum and Kuehn, 2011). There is however a general agreement on the fact that the branches used to describe alternative interpretations (or values of a parameter affected by epistemic uncertainty) must be mutually exclusive and collectively exhaustive (Bommer and Scherbaum, 2008). This means that while processing the logic tree, once you choose one option in the implementation of a model you automatically exclude the other possible interpretations (mutual exclusivity) and that the set of options described by the different branches represents the entire group of options admitted (collective exhaustiveness). While the first assumption is relatively easy to accept - although it presumes the lack of correlation between the uncertainties in the different branches - the second one certainly has implications that are more difficult and delicate to go along with since it presumes a comprehensive knowledge of a specific model uncertainty, knowledge that cannot be assumed a priori.
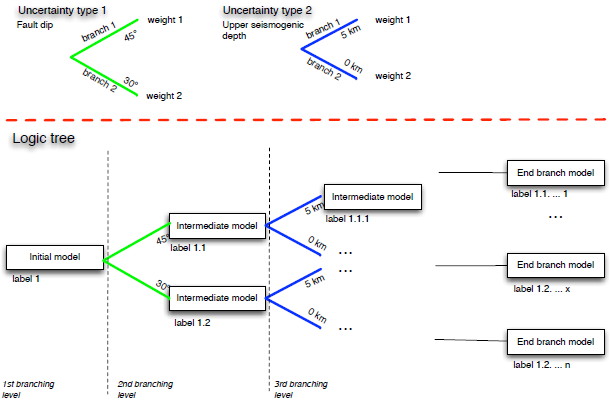
An example of modular logic tree structure supported by the OpenQuake engine. The upper part of the figure contains two modules, one modeling the epistemic uncertainty on the dip angle of a fault, the other modeling the uncertainty on faults upper seismogenic depth.#
The OpenQuake engine logic-tree structure#
The OpenQuake engine offers a flexible and modular methodology to create customised logic-tree structures. The main components of this structure are (see for example the figure above):
branch
It is the elemental component of a logic-tree. A branch represents one possible interpreta- tion of a model or parameter affected by epistemic uncertainty. It is uniquely defined by a tuple consisting of a value and a real number in [0, 1] that can be either be considered a degree of confidence or a probability.
branchset
A branchset is a group of branches which collectively describes the (epistemic) uncertainty associated with a parameter or a model; the sum of weights for the branches within a branchset must be equal to one.
The logic-tree is the combination of a set of linked modules which starting from the roots specify the structure until the uppermost branches. A branchset can applied to all the sources included in the initial seismic source model, to a subset of sources, to a branch included in a branchset occurring before in the logic tree structure or even just to a single source. Currently, the rules controlling the application of a branchset incorporated into the OpenQuake engine are the following:
applyToBranches
The current branchset is applied to one or more branches of the previous branching level designated through their unique ID;
applyToSources
The current branchset is applied to one or more sources included in one of the initial seismic source models and designated through their unique ID;
applyToSourceType
The current branchset is applied to all the sources of a specific type (e.g. simple fault sources) included in one of the initial seismic source models;
applyToTectonicRegionType
The current branchset is applied to all the sources belonging to a selected tectonic region type (e.g. stable continental).
The schematic represented in Figure 5.1 shows an example of the conceptual model adopted to describe a logic tree structure.
The seismic source model logic tree#
The seismic source model logic tree handles the epistemic uncertainties related to the definition of geometry, position and seismicity occurrence properties of seismic sources capable of generating ground-motion of engineering relevance at the investigated site.
By default, the first branching level of a seismic source model logic tree contains one (or several) initial seismic source model. Currently is not possible to create a logic tree model by incrementally adding different sources as - for example - in the case of some of the logic tree structures included in the recently presented CEUS-SSC model (Central and Eastern United States Seismic Source Characterization for Nuclear Facilities. 2012). This functionality will be added into future versions of the software.
Supported epistemic uncertainties
The OpenQuake engine supports multiple types of uncertainties in the logic tree branchsets. You can see the full list of available uncertainties with the command:
$ oq info uncertainty_types
At the time of writing (engine v3.24) there are 23 uncertainty types:
01 abGRAbsolute
02 abMaxMagAbsolute
03 applyToTectonicRegionType
04 areaSourceGeometryAbsolute
05 bGRAbsolute
06 bGRRelative
07 characteristicFaultGeometryAbsolute
08 complexFaultGeometryAbsolute
09 extendModel
10 gmpeModel
11 incrementalMFDAbsolute
12 maxMagGRAbsolute
13 maxMagGRRelative
14 maxMagGRRelativeNoMoBalance
15 recomputeMmax
16 setLowerSeismDepthAbsolute
17 setMSRAbsolute
18 setUpperSeismDepthAbsolute
19 simpleFaultDipAbsolute
20 simpleFaultDipRelative
21 simpleFaultGeometryAbsolute
22 sourceModel
23 truncatedGRFromSlipAbsolute
You can see examples in the demos/hazard directory and in the directory qa_tests_data/logictree. Here we will document only the simplest uncertainty types.
sourceModel
This branchset allows the user to load one or several initial seismic source models. Using this module it is possible to use models with different source geometries and properties based on distinct assumptions or interpretations.
bGRRelative
This branchset adds (or subtracts) a delta to the b-value of the double truncated Gutenberg-Richter relationship.
bGRAbsolute
This branchset assigns a specific value of the b-value of the double truncated Gutenberg-Richter relationship.
maxMagGRRelative
This branchset considers the epistemic uncertainty on the maximum value of magnitude used to define a double truncated Gutenberg-Richter distribution. The application of this branchset adds (or subtracts) a delta value to the maximum magnitude.
maxMagGRAbsolute
This branchset considers the epistemic uncertainty on the maximum value of magnitude used to define a double truncated Gutenberg-Richter distribution. The application of this branchset assigns a specific value of the maximum magnitude of a double truncated Gutenberg-Richter.
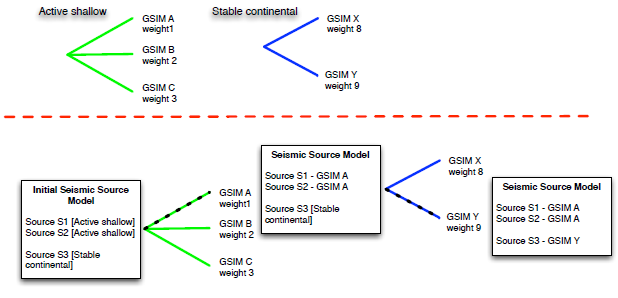
(upper panel) Example of branchsets belonging to the ground-motion logic tree. (lower panel) Example of ground-motion logic tree processing. The initial seismic source model, on the left, is propagated through a simple logic tree structure following the path indicated by the black dashed line. Model information is added incrementally as the input models propagate through the tree structure. In this example hazard is compute using GSIM A for the sources in active shallow tectonic region and GSIM Y for sources in stable continental region#
Note that the rules defined by each branchset are applied to the sources in the input model matching one of the filters. If a branch set has not a filter, then the associated epistemic uncertainty will be applied to all the sources included in the seismic source model.
The ground-motion model logic tree#
The current structure of the ground-motion model logic tree is simple and designed to support just the use of alternative GSIMs models for a single tectonic region.
Supported epistemic uncertainties
The epistemic uncertainty allowed for the GSIM logic-tree is the following:
gmpeModel
This module assigns to each tectonic region one or many GSIMs. This branchset implicitly contains a filter since it is applied only to the seismic sources belonging to the corresponding tectonic region. The example within the figure above illustrates the common processing of the ground-motion logic tree operated by the OpenQuake engine. In this example the source model contains seismic sources included in two tectonic domains: active tectonics and stable continental. The branchset defined for ’active shallow’ is therefore applied just to sources ’S1 and ’S3’ while the branchset for sources in stable continental regions is utilized only for source ’S3’.
Logic tree processing#
The OpenQuake engine currently provides two distinct ways to process logic-trees: full-path enumeration and Monte Carlo sampling.
Full path enumeration is a methodology which generates all the models admitted by a logic tree structure. For this reason, the use of this methodology is feasible only when the logic tree structure is relatively simple, that is when the number of end branches is at maximum in the order of a few tens.
Monte Carlo sampling is instead a methodology which makes an extensive use of random number generation in order to select a subset of models capable to reliably define the overall uncertainty on the final results produced by the epistemic uncertainties used in the construction of the logic tree structure.
In the following sections we provide a short description of the these two methodologies as implemented in the OpenQuake engine.
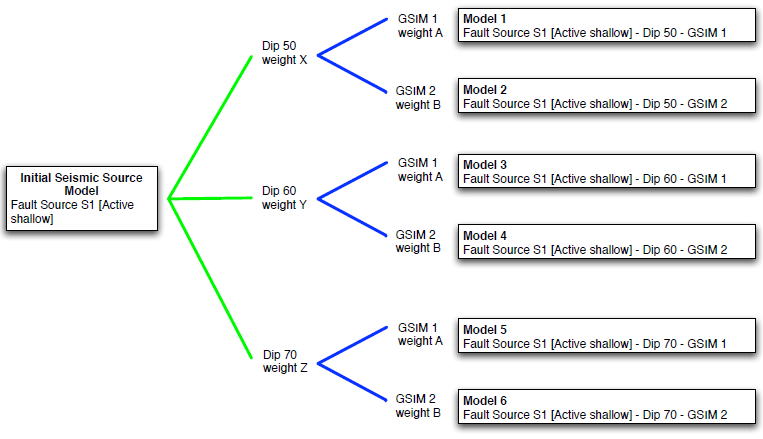
Logic tree full path enumeration processing. Note that the first branching level, the one dealing with the definition of the initial seismic source model is neglected since we assume there is no epistemic uncertainty associated with its definition. The final PSHA input model contains the initial sources each one with an associated GSIM to be used in the calculation of hazard for this specific logic tree path.#
Full-path enumeration#
Full-path enumeration is the simplest methodology implemented in the OpenQuake engine for logic-tree processing. As previously anticipated, it consists of computing hazard for the entire set of investigated sites using all the possible paths admitted by the specific logic tree structure defined. Let’s consider the example described in the figure above to illustrate how this method operates.
The logic structure depicted in this figure contains two branching levels each one including a single branchset. Note that for the sake of simplicity and clarity we assume that the first branching level (i.e. the one used to define the initial seismic source model) is not affected by epistemic uncertainty. Note also that the initial seismic source model contains only one fault source. The branchset in the first branching level describes the epistemic uncertainty on the dip angle; three values, each one with an associated probability, are considered plausible. The second branchset describes the epistemic uncertainties associated with the modelling of ground-motion; two GSIMs are admitted in this case. On the right side of the figure the entire set of models originated by the logic tree structure are briefly described in terms of their distinctive parameters.
Monte Carlo sampling#
The Monte Carlo sampling of the logic tree is implemented in a simple and straightforward way. Given a branchset, following the same order used to add the branches we create a cumulative distribution function like the one represented by the red bars in the figure below. A sample model is then obtained from this distribution simply via the generation of a random number (i.e. a real number in the interval [0.0, 1.0]) and the identification of the interval in the cumulative distribution which includes it. In the figure below the endpoints of the intervals are represented with horizontal dashed segments. Let’s assume for example that the random number generator gives a value equal to 0.6. As clearly visible on the y-axis, this value falls within the interval relative to branch ’b9’. Following samples will be generated by repeating the same procedure as many times as needed. Clearly the higher is the weight associated with a branch the higher will be its probability of being sampled. In the example figure the branch with the higher weight is ’b5’.
A full path over the logic tree structure is built starting from the initial seismic source model and repeating this sampling procedure at each branching level.
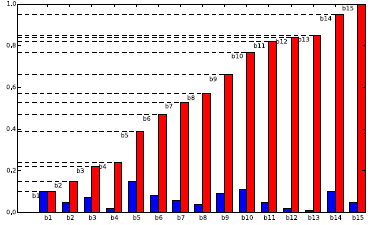
On the x-axis an hypothetical list of branches included in a branchset. The height of the blue bar is proportional to the corresponding weight. The red bars show the cumulative distribution function.#
Calculation of mean and percentiles/quantiles#
The calculation of statistical parameters on the computed hazard results is done using the following approach.
From the set of hazard curves computed at a specific site we select the probabilities of exceedance for a given intensity measure level \(P=\{poe_1,poe_2,..,poe_n\}\) where \(n\) is the number of realisations i.e. hazard results obtained by processing the logic tree.
In case of a full path enumeration processing methodology, we arrange \(P\) in ascending order and we change the order of the corresponding weights accordingly. Using these weights we compute the cumulative distribution function (CDF). We intepolate the curve defined by the CDF and the probabilities of exceedance (poes) to obtain the values of poes corresponding to the quantiles defined by the user. Using the computed values of the probability of exceedance we find the corresponding curves.
In case of a logic tree processing based on a Monte Carlo sampling the quantiles are computed from this set of probabilities using standard methodologies.
