Computing capacity curves#
Capacity curve definition#
The hysteresis behaviour of each SDOF oscillator (one per building class) was defined based on the associated capacity curve, expressed in terms of spectral acceleration (Sa), versus spectral displacement (Sd). For the building classes where no significant reduction in the base shear capacity due to damage accumulation was expected (e.g. steel frames, timber and composite structures) the capacity was assumed to follow a trilinear elasto-plastic model (see Figure 1). The curves were defined based on the yielding (Sdy) and ultimate (Sdult) displacements and the elastic (T1) and yielding (Ty) periods. When a formula to directly calculate the yielding period was not available, it was assumed that Ty is equal to 1.5 times T1 (e.g. Calvi et al. 2006, Crowley and Pinho 2006).
Building classes for which a significant reduction in the base shear capacity is expected due to the accumulation of damage in masonry panels (e.g. confined masonry or reinforced concrete with infills, (e.g. Dolšek and Fajfar 2008, Riahi et al. 2009) were modelled assuming a quadrilinear capacity curve (as depicted in Figure 1). The reduction in the displacement capacity due to the additional stiffness from the masonry walls was modelled using the reduction factors proposed by Bal et al (2010).
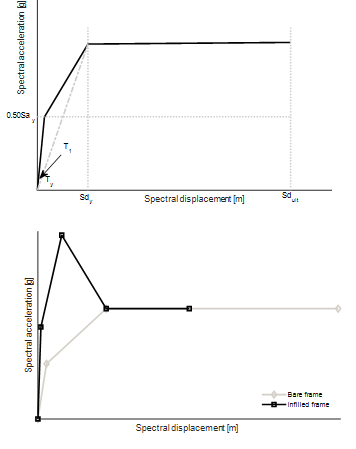
Figure. 1 Example of capacity curves of bare frame vs infilled frames considering reduction on initial stiffness (adapted from Martins and Silva (2020)).
In Acceleration Displacement Response Spectrum (ADRS) format, the mean capacity is estimated from the roof displacement (δr) of the multi-degree-of-freedom structure considering the relationships listed below, where (T) is the period of vibration and (Г) the first mode participation factor
P-Delta effects#
To simulate the effects of second order nonlinearities in the equivalent SDOF models a series of modifiers to the ultimate drift were defined. These modifiers originated from the capacity curves developed by Romao et al 2021. From each capacity curve the ultimate drift was computed and the respective ratio to the ultimate drift of a one storey structure was evaluated, resulting in the values listed in Table 1. The incorporation of P-Delta effects in masonry building classes followed a similar approach this time using the HAZUS manual (FEMA 2014) as reference to estimate the reduction of displacement capacity with height (see Table 2).
Table 1. Multipliers used to estimate ultimate displacement considering P-Delta effects for building classes other than Masonry
No Storeys |
Reduction factor (no seismic provisions) |
Reduction factor (with seismic provisions) |
|---|---|---|
1 |
1 |
1 |
2 |
0.94 |
0.95 |
3 |
0.87 |
0.9 |
4 |
0.81 |
0.85 |
5 |
0.74 |
0.81 |
6 |
0.71 |
0.78 |
7 |
0.67 |
0.75 |
8 |
0.64 |
0.73 |
9 |
0.6 |
0.7 |
10 |
0.57 |
0.68 |
11 |
0.53 |
0.65 |
12 |
0.5 |
0.63 |
12+ |
0.5 |
0.63 |
Table 2. Multipliers used to estimate ultimate displacement considering P-Delta effects for masonry building classes
No Storeys |
Reduction factor |
|---|---|
1 |
1 |
2 |
1 |
3 |
0.83 |
4 |
0.75 |
5 |
0.67 |
6 |
0.50 |
6+ |
0.50 |
References#
Bal, I.E., Bommer, J.J., Stafford, P.J., Crowley, H. and Pinho, R. (2010) The influence of geographical resolution of urban exposure data in an earthquake loss model for Istanbul. Earthquake Spectra, 26(3): p. 619-634. DOI: 10.1193/1.3459127.
Calvi, G., Pinho, R. and Crowley, H. (2006) State-of-the-knowledge on the period elongation of RC buildings during strong ground shaking.
Crowley, H. and Pinho, R. (2006) Simplified equations for estimating the period of vibration of existing buildings. in Proceedings of the 1st European Conference on Earthquake Engineering and Seismology.
Dolšek, M. and Fajfar, P. (2008) The effect of masonry infills on the seismic response of a four-storey reinforced concrete frame — a deterministic assessment. Engineering Structures, 30(7): p. 1991-2001. DOI: http://dx.doi.org/10.1016/j.engstruct.2008.01.001.
FEMA (2014) HAZUS-MH MR5, Technical Manual, Department of Homeland Security - Federal Emergency Management Agency
Martins, L. and Silva, V. (2020) Development of a fragility and vulnerability model for global seismic risk analyses. Bulletin of Earthquake Engineering. DOI: 10.1007/s10518-020-00885-1.
Riahi, Z., Elwood Kenneth, J. and Alcocer Sergio, M. (2009) Backbone Model for Confined Masonry Walls for Performance-Based Seismic Design. Journal of Structural Engineering, 135(6): p. 644-654. DOI: 10.1061/(ASCE)ST.1943-541X.0000012.
Romão, X.,Pereira, N., Castro, J.M., Crowley, H., Silva, V., Martins, L. and De Maio, F. (2021). European Building Vulnerability Data Repository. Zenodo. https://doi.org/10.5281/zenodo.4062410

