Vulnerability analysis

Vulnerability curves provide the expected level of loss for a given level of ground shaking. The most frequent method to estimate vulnerability is through the convolution between fragility functions and a damage-to-loss model.

Damage to loss models

Damage-to-loss models (also know as consequence models) establish the connection between the level of damage and the expected loss (see examples in Figure 1).

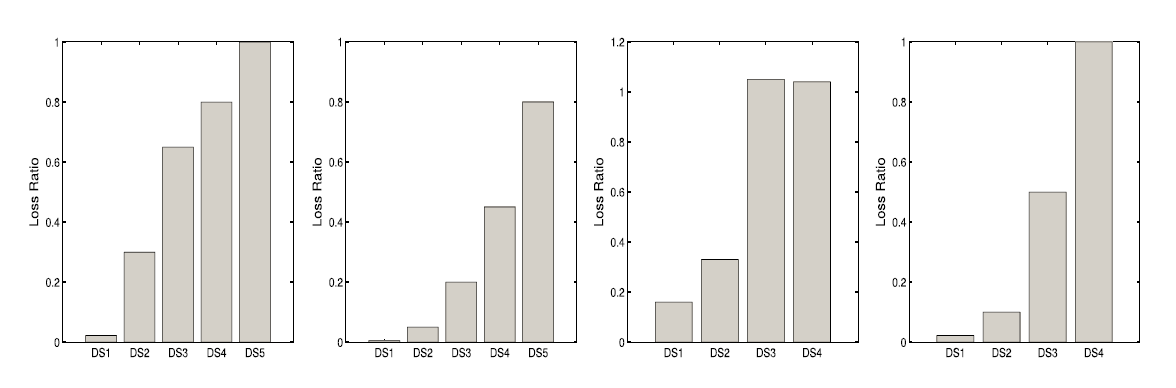Figure. 1 Example of damage-to-loss models. From left to right: Di Pasquale and Goretti (2001) (Italy); Kappos et al. (2006) (Greece); Bal et al. (2008) (Turkey) and HAZUS (FEMA 2014) (California).

Uncertainty around the mean loss can be modelled through a beta distribution (Martins et al 2016).

Computing vulnerability curves

Converting fragility into vulnerability functions is then numerically performed from the equation below using a damage-to-loss model that correlates each damage state with the respective probability distribution of loss ratio.

\[E[LR|IM]=\sum_{i=1}^{nDS}\sum_{j=1}^{m}\left(P[DS=ds_i|IM]*LR_{i,j}*P[LR_{i,j}\right)\]

Standard deviation on expected loss

When not explicitly modelled, the uncertainty in the mean loss ratio can be estimated from the equation by Silva (2019) (see below)

\[\sigma_{LR}|GMR=\sqrt{E[LR_{GMR}|IM]*\left(-0.7-2*E[LR_{GMR}|IM]+\sqrt{6.8*E[LR_{GMR}|IM]+0.5}\right)}\]

References

Bal İE, Crowley H, Pinho R, Gülay FG. (2008) Detailed assessment of structural characteristics of Turkish RC building stock for loss assessment models. Soil Dynamics and Earthquake Engineering; 28(10–11):914–932.DOI:10.1016/j.soildyn.2007.10.005.

Di Pasquale G, Goretti A. (2001) Vulnerabilità funzionale ed economica degli edifici residenziali colpiti dai recenti eventi sismici italiani in Proceedings of the 10th National Conference ‘L’ingegneria sismica in Italia’. Potenza-Matera, Italy

FEMA. (2014) HAZUS-MH MR5, technical manual, Department of Homeland Security—Federal Emergency Management Agency

Kappos A, Panagopoulos G, Panagiotopoulos C, Penelis G. (2006) A hybrid method for the vulnerability assessment of R/C and URM buildings. Bulletin of Earthquake Engineering; 4(4):391–413. DOI:10.1007/s10518-006-9023-0.

Martins, L., Silva, V., Marques, M., Crowley, H. and Delgado, R. (2016) Development and assessment of damage-to-loss models for moment-frame reinforced concrete buildings. Earthquake Engineering & Structural Dynamics, 45(5): p. 797-817. DOI: 10.1002/eqe.2687

Silva, V. (2019) Uncertainty and correlation in seismic vulnerability functions of building classes. Earthquake Spectra DOI: 10.1193/013018eqs031m.